Oscillatore Armonico con Forza costante. Esercizio con Simulazione
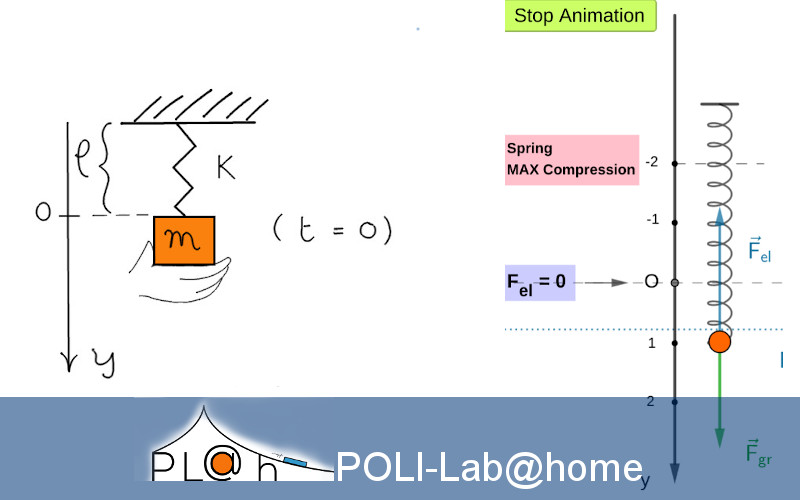
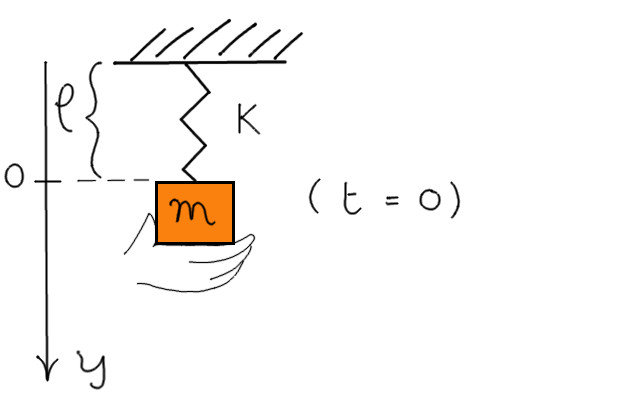
Una massa è collegata a una molla di costante elastica k come mostrato in
figura. All’istante t = 0 la molla è in condizione di riposo (forza elastica = 0) e la massa è in quiete sostenuta da una mano. Supponendo che nello stesso istante la mano sia tolta, quale tra le seguenti è l’equazione differenziale che descrive il moto della massa?
- \( mg-ky=m\ddot y\)
- \( -ky=m\ddot y\)
- \( mg-k(y-l)=m\ddot y\)
- \( k(y-l)=m\ddot y\)
Dopo aver individuato l’equazione corretta, prova a risolverla.
Qui sotto trovate un’applicazione che consente di simulare la situazione proposta nell’esercizio e anche di esplorare situazioni in cui la posizione di partenza non sia y=0 (‘Set initial position: y(0)’). Tra le altre cose essa permette di osservare come la frequenza del moto (la \(\omega\), se volete) cambi al variare della costante elastica K e della massa m.
Qui il link alla soluzione del quesito e alla soluzione dell’equazione differenziale.