21-July. Basic Concepts 1. Fourier’s law

Consider a wall with different temperatures at its sides,
T\( _B \) > T\( _A \) .
Let be \( \Delta\)x its thickness.
Heat will flow through the wall from the hot side to the cold side. The amount of heat that flows per unit time and per unit surface is the Heat Flow density q (the term ‘density” refers to the fact that we are considering the flow through a unit surface, is a surface density of heat flow).
The Heat flow density q turns out to be proportional to the temperature difference \( \Delta\)T and inversely proportional to the wall thickness \( \Delta\)x . Be \( \lambda\) the constant of proportionality.
\(q=-\lambda \,\frac{\Delta T}{\Delta x}\)
This relation is called Fourier’s Law, \( \lambda\) is the thermal conductivity; we can deduce its units from the Fourier’s Law: W/(m K). The thermal conductivity depends on the material of the wall. Materials with high values of \( \lambda \) have a great ability to conduct heat.
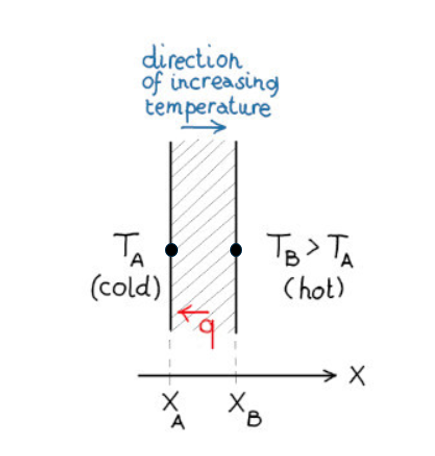
The minus in the equation means that the direction of the heat flux is opposite to the direction in which \( \Delta T \) is positive, i.e. to the direction of increasing temperature: heat flows naturally in the direction of decreasing temperature!
UNITS
Units are important to carry out reliable estimates. Let’s be clear about the units of some important physical quantities involved in these few lines:
| Heat | J | Thermal Energy |
| Temperature T | K or °C | Using Kelvin or Celsius degrees is the same |
| Thickness \(\Delta \)x | m | |
| Power | J/s=W | Energy per unit time |
| Heat Flow density q | W/m\(^2\) | Energy per unit time and per unit area flowing through a wall |
| Thermal Conductivity \( \lambda \) | W/(mK) |
