Uno sguardo alle Reti Neurali

Una Rete Neurale Artificiale (Artificial Neural Network, ANN) è un sistema capace di svolgere calcoli e risolvere alcune categorie di problemi tipicamente risolti da sistemi intelligenti. Perché il nome Rete Neurale? Semplice, come vedremo fra poco, si ispira ai principi di funzionamento delle reti neurali biologiche
In questo post cercheremo di dare una breve spiegazione del loro funzionamento senza entrare nei dettagli. Una sorta di primo incontro con questi sistemi computazionali, utile per avere un’idea generale e per iniziare a “giocarci” avendo una minima cognizione di quel che facciamo. Per essere chiari, questo primo contatto con il mondo dell’Intelligenza Artificiale è da inquadrare nell’ambito del Corso “Dalle Leggi di Conservazione alla Scoperta scientifica“. È pensato per mettere gli studenti in condizione di poter usare una semplice rete neurale per l’analisi di eventi di collisione in fisica delle particelle (vedi il post Fisica & Intelligenza Artificiale).
Lo schema qui sotto rappresenta un modello di rete neurale detta Multilayer Perceptron. I nodi colorati che vedete sono “neuroni”. La rete va letta da sinistra verso destra. Puoi scaricare l’immagine della rete neurale e il Flowchart della ANN, cliccando qui.
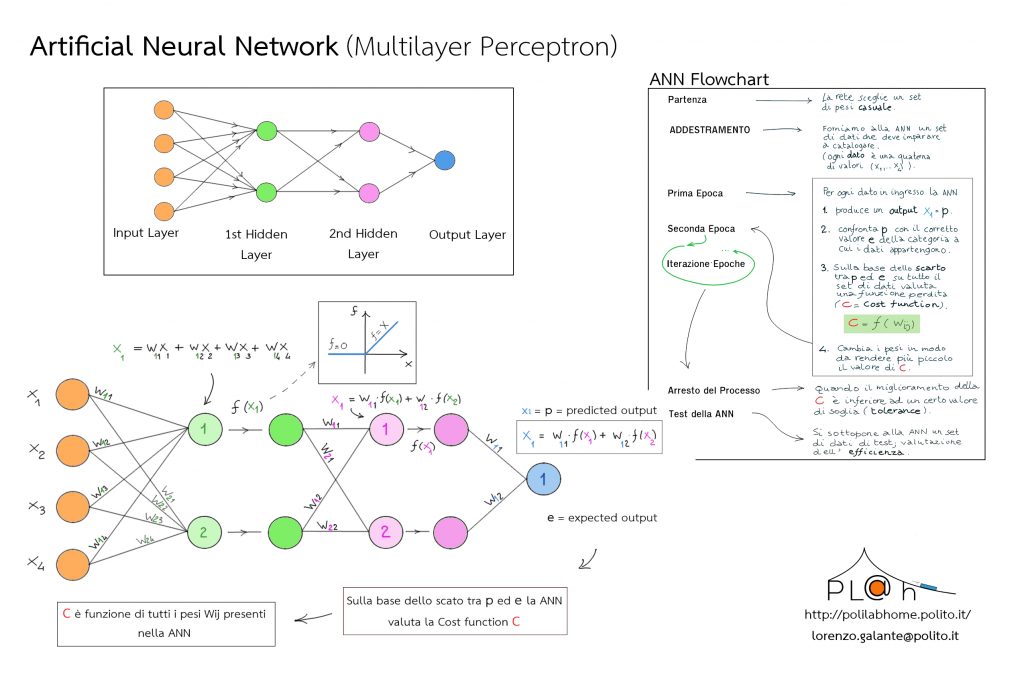
Leggiamo la ANN… da sinistra a destra
Il primo strato di neuroni (Input Layer), nodi arancioni, è composta da un certo numero di neuroni di input. Questi hanno l’unico scopo di fornire un valore numerico in ingresso. Indichiamo il valore di ciascun neurone di input con \(x_i\). Ogni neurone di questo strato invia il suo valore \(x_i\) a ogni neurone dello strato successivo (questo spiega le linee di collegamento). Se \(n\) è il numero di neuroni di input e \(m\) il numero di neuroni dello strato successivo abbiamo \(n\,m\) connessioni tra i due strati. Come vedremo tra breve, in realtà, il segnale inviato non è esattamente \(x_i\). È piuttosto \(x_i\) moltiplicato per un peso w (con valore tra 0 e 1).
Lo strato verde successivo è il primo Hidden Layer (Strato Nascosto). I neuroni di questo layer iniziano ad avere un comportamento interessante e diverso da quello dei neuroni di input:
- Ricevono un valore in ingresso e si attivano di conseguenza. Per esempio il valore di ingresso, x1, del neurone 1 è la somma pesata dei valori di input che lo raggiungono:
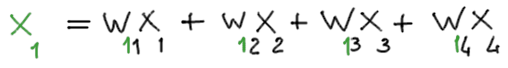
I pesi ( w11, w12, w13, w14 ) sono numeri compresi tra 0 e 1 che definiscono la “forza”o l’importanza del valore (segnale) che i neuroni 1, 2 , 3 e 4 inviano al neurone 1 dell’hidden layer. L’indice verde indica il neurone dell’hidden layer che riceve (il numero 1 in nell’esempio), gli indici neri (1, 2, 3, 4) esprimono da quali neuroni giunge il segnale.
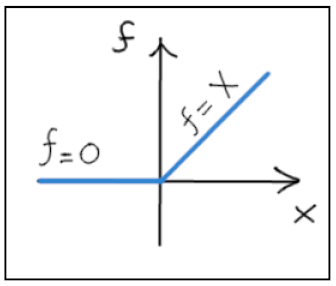
- Inviano un segnale in uscita che dipende dal segnale x1 ricevuto in ingresso. Il valore del segnale in uscita è deciso da una funzione di attivazione f(x) che agisce sulla x1 in ingresso. Nel nostro esempio essa è la cosiddetta ReLU: fornisce il valore 0 se x1<0, un valore uguale a x1 se x1>0.
A livello molto grezzo questo è quel che fanno le cellule neuronali di un sistema biologico. Ricevono segnali in ingresso provenienti da altri neuroni (grazie ai dendriti) e, sulla base del segnale “somma” dei vari segnali si attivano. Cioè inviano un loro segnale verso l’esterno (attraverso l’assone).
Veniamo al secondo Hidden Layer. Esso si comporta esattamente come il primo strato nascosto che abbiamo appena discusso. Stessa funzione di attivazione
L’unica differenza è che, in ingresso, riceve i segnali inviati dai neuroni del primo hidden layer, pesati con un nuovo set di pesi: w11, w12. Per esempio, il valore di ingresso del neurone 1
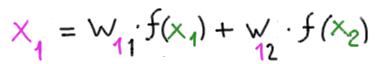
Essendo l’ultimo strato nascosto esso comunica direttamente con il neurone di output (quello blu in fondo alla rete).
Con pesi w11 e w12, l’ultimo hidden layer invia il segnale di ingresso al neurone di output:
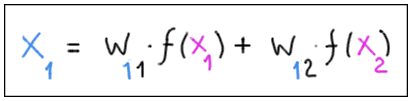
Il neurone di output “assume” il valore x1.
Come la ANN risolve problemi di riconoscimento di pattern
Abbiamo “passeggiato” attraverso la rete neurale dall’input layer all’output layer e abbiamo visto cosa capita alle informazioni in ingresso (gli x1, x2, ..,x4 dei neuroni di input) a mano a mano che ci spostiamo verso il neurone di output. Potremmo sintetizzare in questo modo:
La rete neurale analizzata trasforma (se preferite “mappa”) una serie di valori iniziali (x1, …., x4) in un unico valore finale l’ x1 del neurone di output.
Gli (x1, …., x4) rappresentano il problema.
Il valore del neurone di output, x1, è la soluzione.
Adesso è giunto il momento di spiegare in che senso x1 sia la soluzione al problema e come sia possibile per una ANN raggiungere la soluzione corretta.
Provate a pensare che i dati in ingresso (x1, …., x4) siano valori che definiscono un’immagine (per esempio i valori di intensità in scala di grigi di tutti i pixel dell’immagine (in questo caso un’immagine molto piccola e povera, di dimensione 2×2 e, quindi, con soli 4 pixel). Pensate di catalogare tutte le possibili immagini di questo tipo in 3 categorie: 1, 2 e 3 a piacere. Ebbene il problema che potete porre alla ANN che abbiamo visto insieme è questo: diamo in ingresso alla ANN i valori delle intensità dei 4 pixel dell’immagine (x1, …., x4) e le chiediamo di riconoscere se l’immagine appartiene alla categoria 1, 2 o 3. E la soluzione? L’output della rete deve essere 1 o 2 o 3 a seconda che l’immagine in ingresso appartenga alla prima, alla seconda o alla terza categoria.
È ovvio che se ci limitassimo a fornire i dati in ingresso alla nostra ANN strutturata con un set casuale di pesi dei vari collegamenti inter-neuronali la soluzione x1 fornita sarebbe casuale e molto probabilmente sbagliata. Manca ancora qualcosa di fondamentale: La ANN va addestrata!
Addestramento di una ANN
La ANN va allenata con un dataset di valori iniziali (nel nostro esempio: i 4 valori dei pixel dell’immagine). Dobbiamo fornire alla rete un certo numero di (x1, …., x4) diversi di cui conosciamo già la categoria di appartenenza e comunicare alla rete quale sia la risposta esatta.
Facciamo un esempio Supponiamo di avere un dataset di addestramento formato da 100 immagini 2×2 di cui conosciamo la classificazione. Vediamo come si svolge l’addestramento.
Partenza
Alla partenza la rete parte con un set di pesi casuali (tutti quelli che vedete nella figura: gli w1i, gli w1i e infine gli w1i)
Inizia la prima Epoca di addestramento
- Le diamo in pasto, una dopo l’altra, le nostre 100 immagini (nel formato (x1, …,x4)). Lei per ognuna delle immagini produce un x1 (che d’ora in poi chiameremo predicted output p).
- Confronta il valore di p di ogni immagine con il valore corretto della categoria di appartenenza, che chiamiamo e (expected output).
- Sulla base dello scarto tra p ed e su tutte e 100 le immagini valuta una funzione di perdita detta Cost function o Loss.
La Cost Function è funzione di tutti i pesi della rete: \(C=f(w_{ij})\)
- Cambia i pesi in modo da Rendere più piccola la Cost Function.
Seconda epoca di addestramento
- La rete ripete le fasi della prima epoca partendo dal nuovo seti di pesi scelto durante l’epoca precedente, quindi un set di pesi che ha ridotto la Cost Function. I pesi sono dunque diversi, …migliori!
- Usa le stesse 100 immagini di prima, ma le considera con un ordine diverso.
- Al termine di questa epoca la rete valuta nuovamente la Cost Function, che se la rete ha scelto bene dovrebbe assumere un valore più piccolo rispetto all’epoca precedente. Quindi cambia ancora una volta i pesi nel tentativo di minimizzarla ulteriormente.
Iterazione delle epoche
Le epoche si succedono una dopo l’altra, l’idea è che ad ogni epoca successiva la ANN sia più brava a riconoscere le immagini e a classificarle sulla base delle categorie 1, 2 o 3.
Come si arresta il processo
Le epoche si ripetono fino a quando il metodo che la rete sta usando per minimizzare la Cost Function non riesce più ad ridurne il valore di una certa soglia stabilita detta tolerance. Oppure la ANN ha raggiunto il massimo numero di iterazioni (epoche) fissato dall’utente.
Test di una ANN
Dopo l’addestramento dobbiamo mettere alla prova la ANN e scoprire con quale efficienza la nostra rete ha imparato a catalogare i dati iniziali nelle tre categorie, in altre parole, a risolvere il problema. Si prende allora un secondo dataset, detto di Test. Lo si sottopone alla ANN addestrata e si valuta quale sia la percentuale di risposte esatte. Nel caso la percentuale non sia soddisfacente si può lavorare su certi parametri che definiscono la ANN stessa nel tentativo di migliorarne l’efficienza.
I principali parametri della ANN
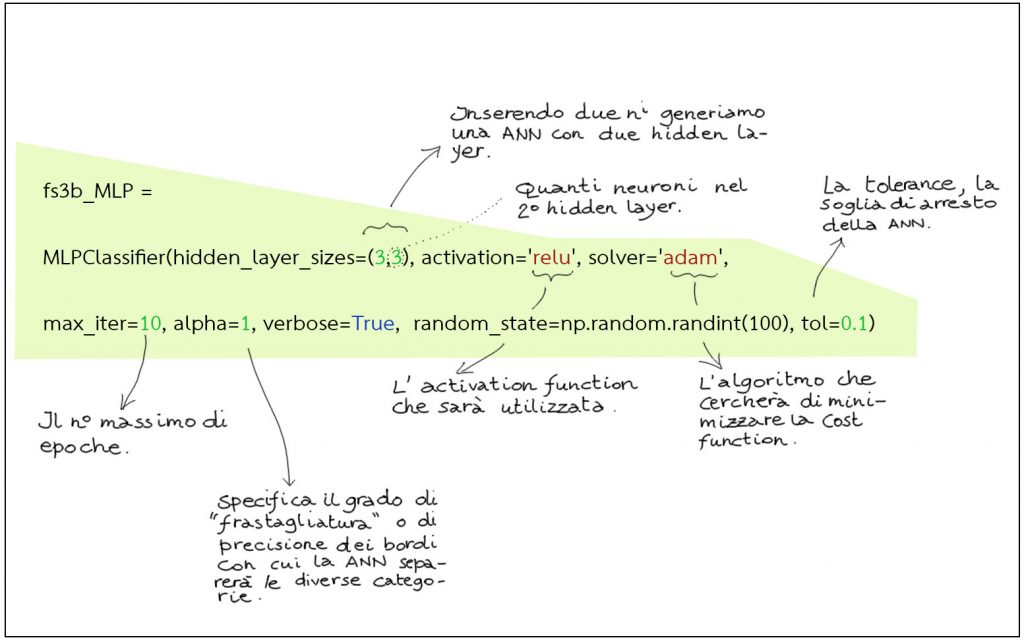
I principali parametri che definiscono una ANN sono elencati qui sotto
Il numero di hidden layer, il numero di neuroni per ogni hidden layer, il numero di epoche (max_iter), il parametro Alpha, la soglia di arresto Tolerance (tol). Nell’immagine qui sotto trovate la riga di codice, commentata, che appare nel programma condiviso a cui potete accedere seguendo la procedura indicata qui).