Cilindro su Piano Inclinato
Affrontiamo insieme un problema cosiddetto di “Corpo Rigido”. Avete a vostra disposizione un’applicazione che vi consente di osservare il fenomeno fisico e di fare qualche piccola “sperimentazione” variando il valore di alcuni parametri. Provate a impostare la soluzione e poi confrontatela con quella pubblicata su questa pagina.
Il testo del problema
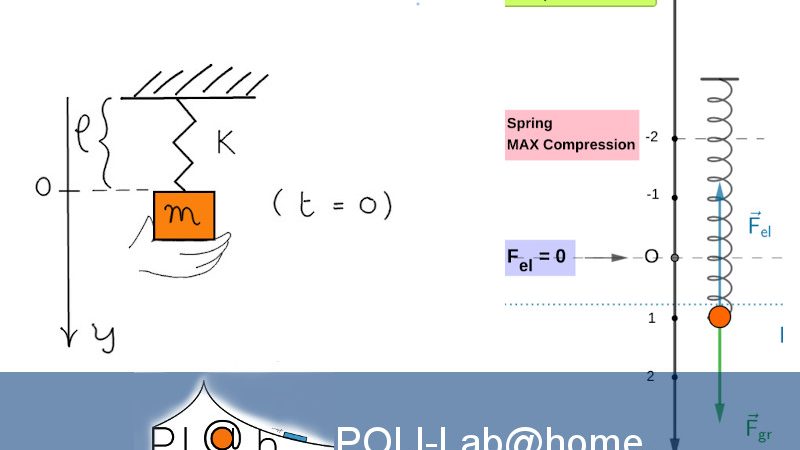
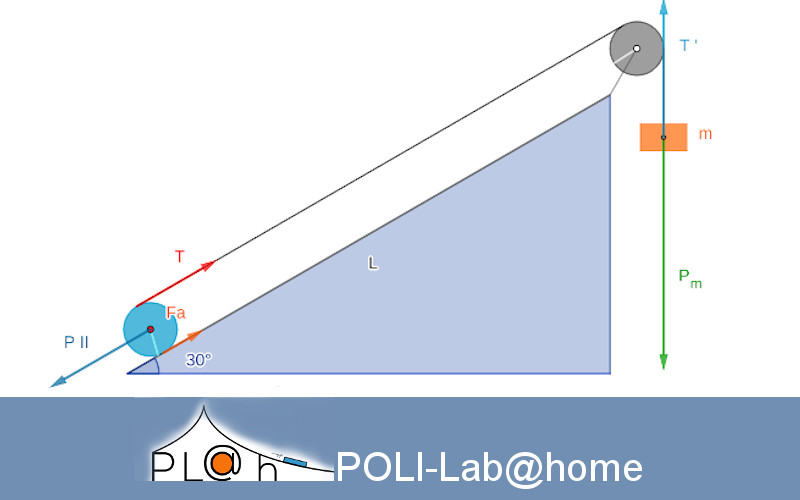
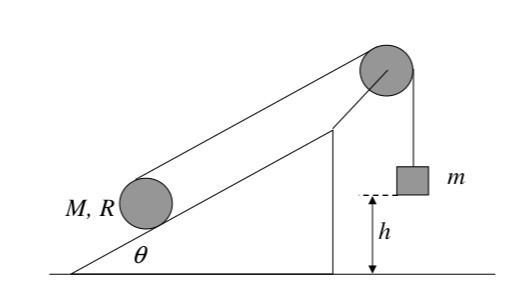
Un cilindro pieno omogeneo di massa \(M\) e raggio \(R \) è posto sopra un piano scabro inclinato di un angolo \(\theta \). Una fune inestensibile e di massa trascurabile è avvolta attorno al cilindro, passa su una carrucola fissa, anch’essa assimilabile ad un cilindro di massa \(M\) e raggio \(R \). La fune sostiene un cubo di massa m inizialmente mantenuto fermo a distanza h dal terreno. Al tempo \(t = 0\) esso viene rilasciato e comincia a scendere, trascinando il cilindro verso l’alto. Si supponga che il cilindro si muova di moto di puro rotolamento e che la fune non scivoli né sul cilindro, né sulla carrucola.
- Determinare il rapporto tra l’accelerazione \(a_m\) del cubo di massa m e l’accelerazione \(a_M\) del cilindro. (2 punti)
- Determinare l’accelerazione \(a_m\) con cui si muove il cubo dopo esser stato rilasciato, in funzione degli altri dati noti (8 punti)
- Trovare il minimo valore che deve avere la massa m per far salire il cilindro lungo il piano. (2 punti)
- Usando considerazioni energetiche, trovare la velocità con cui il cubo arriva a terra. (3 punti)
L’applicazione
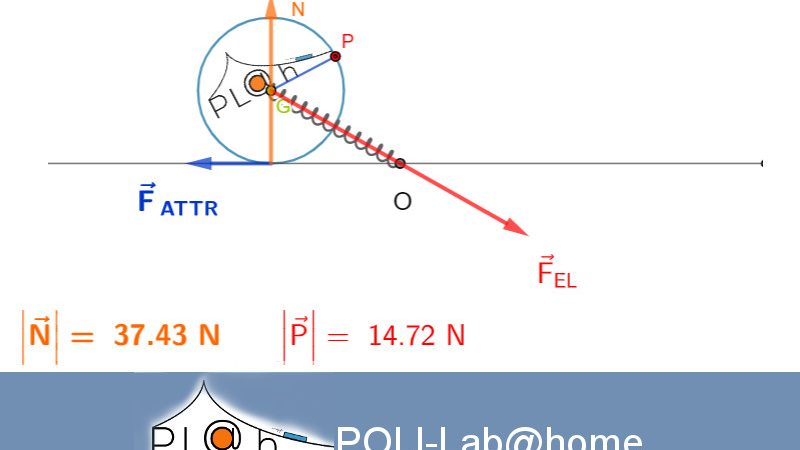
Qui sotto trovate l’applicazione che vi consente di visualizzare e animare il fenomeno con diversi angoli di inclinazione del piano e con diversi valori della massa del blocco sospeso. Essa mostra anche i principali vettori forza agenti sui corpi. Potete osservare e ragionare su quel che capita.
Ragionando di fisica senza formule
- Perché la carrucola ruota più velocemente del cilindro?
- Se l’accelerazione del cilindro è >0 (sale) chi è più grande in modulo tra T e T‘?