Leggi di conservazione in 2D

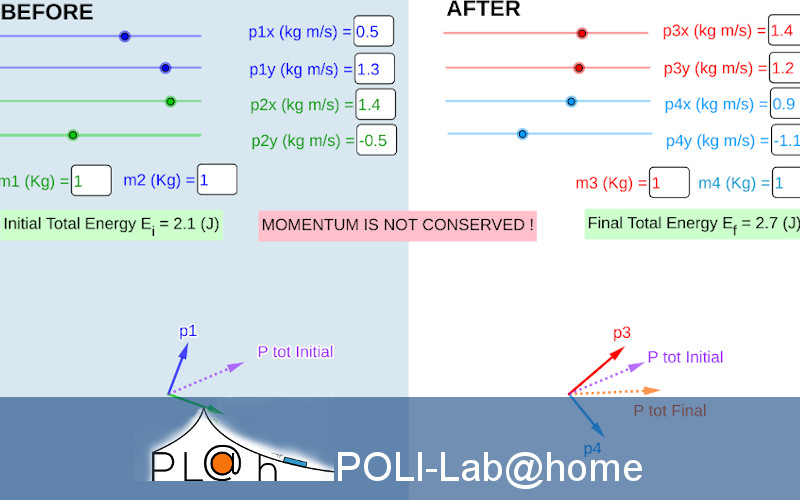
Prendiamo confidenza con le leggi di conservazione nel caso di urti tra due corpi che avvengono su un piano. Per gli urti che considereremo assumiamo che sia valida sia la conservazione della Quantità di Moto (QdM) che la conservazione dell’Energia. In questa pagina avrete a disposizione1 applicazione che vi potrà aiutare a visualizzare e comprendere il significato delle equazioni che chiamiamo leggi di conservazione.Essa vi offre la possibilità di risolvere per via geometrica e visuale le equazioni di conservazione.

Queste sono le equazioni di conservazione (una scalare per l’Energia e una vettoriale per la quantità di moto):

\( \frac{{p_1}^2}{2m_1}+\frac{{p_2}^2}{2m_2} = \frac{{p_3}^2}{2m_3}+\frac{{p_4}^2}{2m_4} \\ \vec{p}_{1}+\vec{p}_{2}=\vec{p}_{3}+\vec{p}_{4} \)

Esse si riferiscono ad un’interazione in cui il numero di corpi prima e dopo rimane sempre lo stesso. Lasciano, però, la libertà di modellare casi in cui le masse dei corpi varino: m1 e m2 sono le masse prima dell’interazione, m3 e m4 quelle dopo.

Sono due equazioni, ma la seconda è vettoriale, dunque, corrisponde a 2 equazioni scalari (caso 2D). In totale abbiamo 3 equazioni scalari:

\( \frac{{p_1}^2}{2m_1}+\frac{{p_2}^2}{2m_2} = \frac{{p_3}^2}{2m_3}+\frac{{p_4}^2}{2m_4} \\ p_{1x}+p_{2x}=p_{3x}+p_{4x} \\ p_{1y}+p_{2y}=p_{3y}+p_{4y}\)

Un esempio di Urto in 2D

Urto tra due monete da 1 centesimo di euro. Un istante prima dell’urto la moneta “bersaglio” ha QdM nulla, mentre la moneta che giunge dallo scivolo ha una QdM diretta verso il segmento lungo tracciato a matita sul foglio A4. All’istante dell’urto si ha conservazione della QdM anche se sul sistema (formato dalle 2 monete identiche) agiscono forze esterne (l’attrito moneta/foglio di carta). Ciò è sostenibile per due motivi: 1. la durata del processo d’urto è così piccola che le forze d’attrito non modificano significativamente le QdM dei due corpi, 2. l’intensità delle forze d’attrito è << delle forze dovute all’urto. In sostanza, appena dopo l’urto i due corpi partono con QdM che rispettano la legge di conservazione.

Se siete curiosi potete realizzare questo esperimento direttamente a casa vostra su un tavolo. Qui trovate dettagli e tutorial che vi guideranno nell’esperimento.

L’ applicazione

L’applicazione vi consente di risolvere le equazioni appena scritte attraverso un processo euristico guidato dalla visualizzazione geometrica dei vettori quantità di moto. Più sotto trovate la descrizione completa e una possibile modalità per usarla.

La sezione BEFORE è dedicata al sistema fisico appena prima dell’interazione. 1. In questa sezione potete determinare le componenti x e y delle quantità di moto di due corpi prima dell’interazione \( \vec{p}_{1} \) , \( \vec{p}_{2} \) e le loro masse \(m_1\), \(m_2\). 2. L’applicazione restituisce il valore dell’energia totale iniziale, così calcolata: \(E_{tot\,In.}=\frac{{p_1}^2}{2m_1}+\frac{{p_2}^2}{2m_2}\). 3. Mostra in blu e verde i vettori \( \vec{p}_{1}\) e \( \vec{p}_{2}\), con un vettore viola tratteggiato la \( \vec{p}_{tot\,In.} \) \( =\vec{p}_{1} +\) \( \vec{p}_{2}\).

La sezione AFTER è dedicata al sistema fisico appena dopo l’interazione. 1. Potete variare le componenti x e y delle quantità di moto dei due corpi appena dopo l’interazione \( \vec{p}_{3} \) , \( \vec{p}_{4} \) e le loro masse \(m_1\), \(m_2\). 2. L’applicazione restituisce il valore dell’energia totale finale. 3. Mostra in rosso e azzurro i vettori \( \vec{p}_{3}\) e \( \vec{p}_{4}\), con il vettore viola tratteggiato ripropone la \( \vec{p}_{tot \,In.} \) e con il vettore tratteggiato arancione la \( \vec{p}_{tot \,Fin.} \)\( =\vec{p}_{3} +\) \( \vec{p}_{4}\). Notate che le masse dei corpi prima e dopo l’urto possono essere definite come diverse (ovviamente sta a voi rispettare la conservazione della massa totale del sistema!)

COME PUÒ ESSERE UTILIZZATA. Impostate una configurazione di quantità di moto per il sistema iniziale e cercate di modificare i parametri del sistema finale in modo che le leggi di Conservazione siano rispettate. Sostanzialmente potete ricercare per via geometrica e visuale soluzioni approssimate del sistema di equazioni di conservazione di Energia e quantità di moto per un interazione tra 2 corpi in 2-Dimensioni. L’applicazione che segue, metterà a vostra disposizione un elemento aggiuntivo: un “Computable Document” che vi consentirà di trovare le soluzioni esatte del sistema di equazioni, potrete così confrontarle con quelle che avete trovato con l’approccio euristico e visuale. ALTRE FUNZIONALITÀ DELL’APPLICAZIONE. Essa fornisce un check logico della conservazione della quantità di moto (entro un certo margine di errore) e della conservazione dell’energia (con un margine d’errore di 0.1 J). Il check sulla quantità di moto è sempre attivo, quello sull’energia è attivabile tramite tasti. INTERVALLI delle GRANDEZZE FISICHE. Le componenti delle quantità di moto iniziali possono variare nell’intervallo [-2, 2]; le masse variano in [1, 5]; le componenti delle quantità di moto finali in [-4, 4].

Visits: 3395