Rotolamento puro
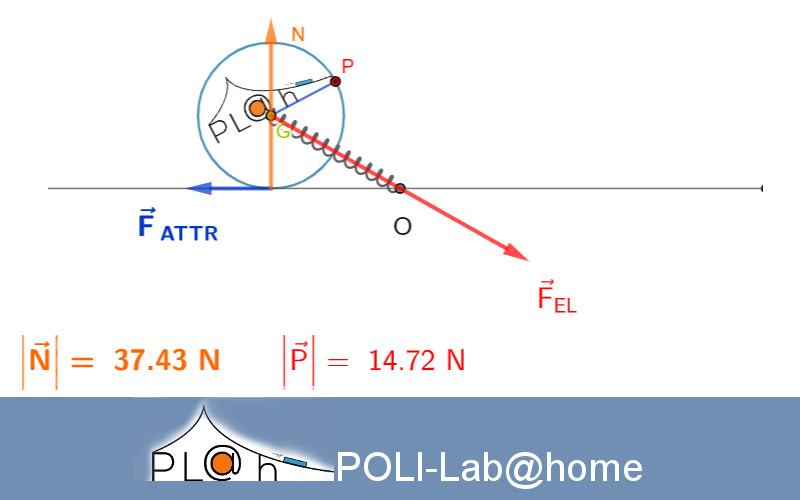
Un disco omogeneo di raggio \(R\) e massa \(m\) rotola senza strisciare su un piano, ed al suo
centro di massa \(G\) è applicata una forza elastica, tramite una molla ideale, di lunghezza a
riposo nulla e costante elastica \(k\), bloccata in un punto \(O\). Inizialmente il disco
è fermo e la posizione del centro di massa, rispetto ad un sistema di riferimento cartesiano
con origine in \(O\) è \(OG = (d;\,R) \) , con \(d >> R\).
- Calcola l’accelerazione angolare e la velocità angolare del disco quando l’ascissa del centro di
massa vale \(d/2\) - Determina la legge oraria del centro di massa del disco (mentre si muove verso sinistra,
prima di urtare contro la parete) - Calcola l’espressione della forza di attrito statico applicata al punto di contatto (mentre
il disco si muove verso sinistra, prima di urtare contro la parete) e, dato il coefficiente di attrito statico \(\mu_S\), determina il valore massimo di \(d\) compatibile con la condizione di rotolamento puro.
Un’appliclazione per esplorare il problema
Attenzione: per questioni di visualizzazione i vettori forza di reazione N e forza peso P sono stati ridotti di un fattore 8.
L’applicazione che vedi qui sotto può essere utile per:
- Visualizzare le forze in gioco e il fenomeno fisico mentre evolve nel tempo.
- Esplorare la dipendenza da parametri quali la massa del disco, la costante elastica, il raggio del disco e la distanza iniziale dall’origine. (1. Variare i parametri all’interno dell’applicazione, 2. Chiedersi come ci si aspetterebbe che cambi l’andamento nel tempo del sistema, 3. Avviare l’animazione e confrontare ciò che si osserva con quanto previsto al punto 2).
- Confrontare alcuni risultati numerici che hai ottenuto con quelli offerti dall’applicazione.
Visits: 30348