Collisioni nucleari (2)

Corso di formazione: La relazione Energia-Impulso di Einstein
Per provare scientificamente la possibilità della produzione di una particella neutra nella collisione abbiamo bisogno di un nuovo strumento di indagine:
il nuovo concetto di Energia che emerge dalla Relatività Speciale di Einstein.
Un breve corso di formazione seguito da una fase di problem solving vi darà il kit minimo di conoscenze necessarie per proseguire l’esplorazione dell’evento che state analizzando.
Premessa sulle unità adottate
Da adesso in avanti tratteremo le grandezze \(E\) (energia), \(p\) (quantità di moto, che chiameremo anche impulso) ed \(m\) (massa) come se fossero delle energie. Ovviamente queste grandezze, eccetto la prima, non sono energie occorre dunque una breve spiegazione del nuovo modo di pensare.
In fisica nucleare l’energia \(E\) si misura in \(eV\) , l’impulso in \(eV/c\) dove \(c\) è la velocità della luce (ricordate che le unità di misura di una massa per una velocità sono identiche a quelle di un’energia divisa per una velocità) e la massa in \(eV/c^2\) (pensate alla formula dell’energia cinetica e ricavate la massa…):
\(E\, \, (eV)\quad \quad\vec{p}\, \, (\frac{eV}{c})\quad \quad m\, \, (\frac{eV}{c^2})\)
Se le volessimo trasformare tutte in energie, potremmo lasciare stare tranquilla così come è l’\(E\), moltiplicare per \(c\) l’impulso \(\vec{p}\), per \(c^2\) la massa. Le grandezze così ottenute sono tutte energie:
\( E \, \, (eV)\quad \quad\vec{p}c \, \, (eV)\quad \quad mc^2 \, \, (eV) \)
Ed ora il tocco di classe! Adottiamo le unità cosiddette naturali in cui \(c=1\). L’effetto netto è che tutte le grandezze appena espresse, si “trasformano” così:
\( E \rightarrow E\,\, (eV)\quad \quad\vec{p}c \rightarrow \vec{p}\,\, (eV)\quad \quad mc^2 \rightarrow m\,\, (eV) \).
\(E\), \(\vec{p}\) ed \(m\) ora sono tutte energie e si possono esprimere in \(eV\). Ovviamente dobbiamo ricordarci che accanto a \(\vec{p}\) è sempre presente il fattore \(1\) (la velocità della luce) e al fianco della massa sta il fattore \(1^2\).
Il Quadrivettore Energia-Impulso
- Ad ogni sistema fisico posso associare un’energia \(E \) e un impulso \( \vec{p}\).
- In Relatività Speciale queste due grandezze formano le componenti di un quadrivettore il cosiddetto quadrivettore Energia-impulso:
\( (E,\,\vec{p} c)\);
in unità naturali:
\( (E,\,\vec{p})\).
- Il quadrivettore Energia-impulso è un vettore in uno spazio a 4 dimensioni, ha infatti 4 componenti: una data dall’Energia, le restanti 3 date dalle 3 componenti dell’impulso. In particolare l’energia costituisce la parte temporale del quadrivettore e l’impulso quella spaziale.
- Sia \(E \), sia \( \vec{p}\) dipendono dall’osservatore inerziale (osservatore in moto rettilineo uniforme) che studia il sistema fisico in questione. Osservatori inerziali diversi daranno valori diversi sia all’energia che all’impulso del sistema e quindi assoceranno ad esso un diverso quadrivettore energia-impulso.
- Einstein ha, però, dimostrato che la differenza dei loro quadrati, che adesso scriviamo in unità naturali,
\( E^2-p^2\)
è un invariante relativistico. Una grandezza, cioè, che assume lo stesso valore in qualsiasi sistema di riferimento inerziale lo si misuri.
- Einstein ha dimostrato quale sia il significato fisico di tale invariante: (sempre in unità naturali) la massa al quadrato del sistema
\(E^2-p^2=m^2\).
Aggiungiamo che l’invariante è in realtà il modulo del quadrivettore energia-impulso (definito mantenendo la distinzione fra le parti spaziale e temporale tramite il segno -). Come nello spazio tridimensionale classico la distanza fra due punti (modulo del vettore spostamento che li congiunge) rimane invariata, così succede per i moduli dei quadrivettori in relatività.
La trasformazione delle componenti di un quadrivettore nel passaggio da un sistema di riferimento inerziale ad un altro in moto con velocità v rispetto al primo viene effettuato utilizzando le trasformazioni di Lorentz. Il modulo del quadrivettore risulterà invariante per tali trasformazioni.
Alcune teorie filosofiche ed il parlare comune asseriscono che secondo la teoria di Einstein “tutto è relativo”. In realtà l’aspetto più interessante è proprio legato all’aver trovato grandezze fisiche che non cambiano a seconda della velocità con cui si muove l’osservatore. Tale invarianza si può interpretare come una simmetria. Simmetria, per capirci, analoga a quel che asserisce ‘un quadrato è invariante per rotazioni di 90° intorno al suo centro’.
PROBLEM SOLVING
La fase di Problem Solving vi vedrà al lavoro con l’applicazione che trovate qui sotto. Essa consente di visualizzare in modo diretto e geometrico la relazione di Einstein (nei paragrafi precedenti abbiamo chiarito il significato dell’ \( m^2\) a secondo membro, da qui in avanti lasceremo cadere il pedice ‘0’ e scriveremo solo \( m\))
\(E^2-p^2=m^2\)
La introduciamo brevemente, dopodiché… buon lavoro con il form dedicato al Problem Solving.
Il quadrato verde ha lato pari all’Energia E del sistema fisico in questione. La sua area rappresenta il termine \( E^2 \).
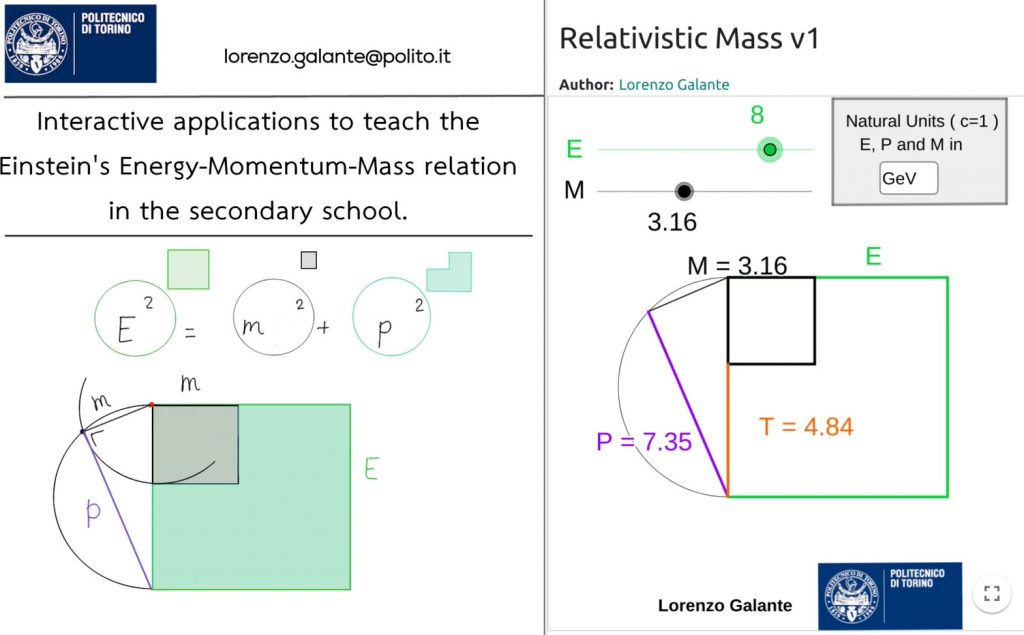
Il quadrato verde ha lato pari all’Energia E del sistema fisico in questione. La sua area rappresenta il termine \( E^2 \) della relazione di Einstein.
Il quadrato nero ha lato pari alla massa m. La sua area corrisponde al termine \( m^2 \)
La differenza delle aree, \( E^2-m^2 \), ha una forma a ‘L’ e nell’immagine qui sopra appare in colore verde acqua: essa rappresenta il termine \( p^2 \). L’applicazione visualizza anche il valore dell’impulso p, che corrisponde alla lunghezza del segmento viola (vedi costruzione geometrica nella figura: triangolo inscritto in semicirconferenza con diametro pari ad E, un cateto è uguale alla massa m… l’altro cateto è dato da \( \sqrt{E^2-m^2} \), dunque rappresenta p). Provate voi a immaginare quale sia il significato fisico del segmento arancione di lunghezza T.
Problem Solving
.
