Equazioni Orarie parametriche

Due esempi e due applicazioni per visualizzare traiettorie piane, espresse con equazioni parametriche in coordinate polari e coordinate cartesiane.

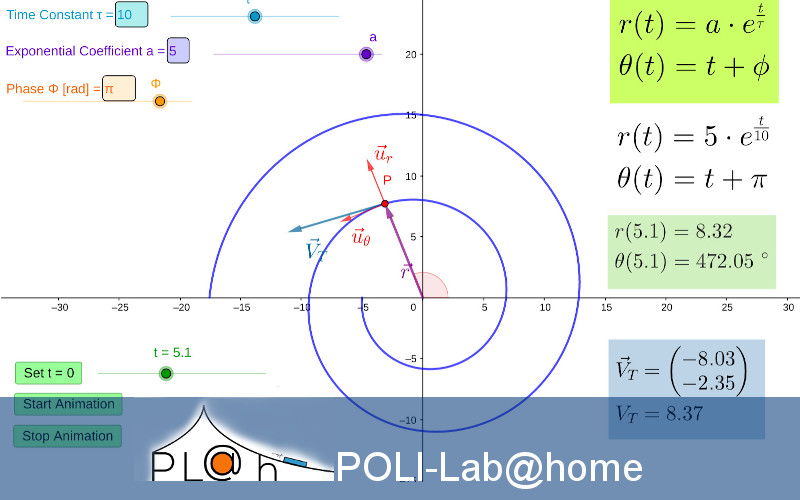
Legge oraria parametrica in coordinate polari

L’applicazione mostra le equazione oraria in coordinate polari ( $r(t), \theta (t)$ ) di un punto che si muove sul piano (x,y). Il raggio $r(t)$ è la distanza dall’origine e cresce esponenzialmente secondo la legge

$r(t)=a \cdot e^{\frac{t}{\tau}}$

L’applicazione consente di variare sia $a$, sia $\tau$, di prevedere e poi verificare gli effetti di tali modifiche.

$\theta (t)$ è la posizione angolare del corpo in moto, ovvero l’angolo che il suo vettore posizione $\vec{r}$ forma con la direzione positiva dell’asse x. Essa varia linearmente secondo la legge

$\theta (t) = t +\pi$

In rosso, istante per istante, sono mostrati i versori radiale $\vec{u}_r$ e trasverso $\vec{u}_\theta$ (tenete conto che sono ingranditi di un fattore 4 per motivi legati alla visualizzazione). In azzurro è visualizzata la velocità tangenziale $\vec{V}_T$.

Legge oraria parametrica in coordinate cartesiane

Il moto di un corpo sul piano x,y può essere descritto da due equazioni che esprimono la variazione nel tempo dell’ascissa e dell’ordinata. Le equazioni si chiamano allora equazioni parametriche del moto in coordinate cartesiane. Il parametro libero di variare è il tempo t.

L’applicazione consente di analizzare la traiettoria di un corpo le cui leggi orarie in x e in y sono due moti armonici sinusoidali.

$x(t) = A \cdot sin(\omega_x \cdot t) \\ y(t)=B \cdot sin(\omega_y \cdot t)$

È possibile variare l’ampiezza e le frequenza angolare dei due moti armonici. Le ampiezze possono variare nel “continuo” in [0,2], le $\omega$ possono assumere solo valori interi in [-2,2].