Theoretical Section

A charged particle, for instance our negative pion (\( \pi^-\)), moves with velocity \(\vec{v}\) in a uniform magnetic field \(\vec{B}\) perpendicular to \(\vec{v}\).

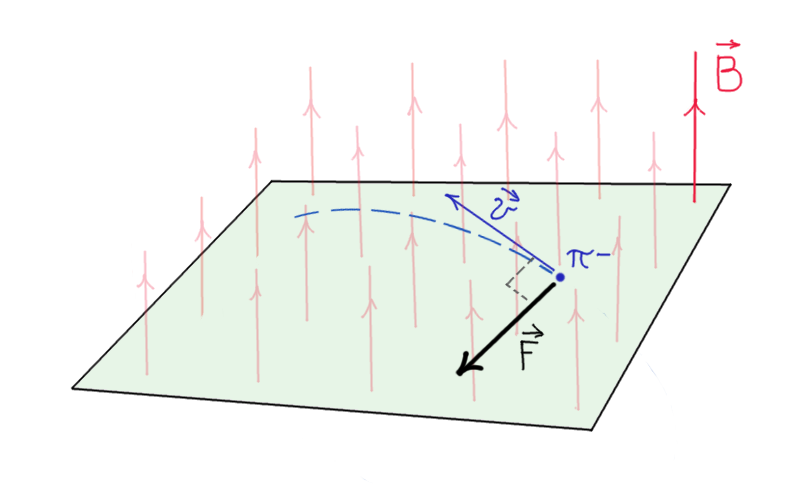
As we know a Magnetic Force \(\vec{F}\) will act on the pion:

\( \vec{F}=q\,\vec{v}\times \vec{B}\).

The pion moves in a chamber filled with He gas. Being charged it electromagnetically interacts with the atomic electrons, thus ionizing the He atoms. The track in the detector is directly given by the ionization path along the pion trajectory.

Since the Magnetic Force acts perpendicularly to \(\vec{v}\) and we can neglect the energy losses due to the ionization process, we can assume that the pion’s speed is constant.

Therefore we have a charged particle moving in a uniform magnetic field, with constant speed. In this situation the Magnetic Force has the following properties:

• \(\vec{F}\perp \vec{v}\)
• \(\vec{F}\) has constant modulus

and may be considered a centripetal force. The following relation holds (remember that the angle between \(\vec{B}\) and \( \vec{v}\) is 90°):

\( qvB=m\frac{v^2}{r}\).

Eliminating \( v\),

\( qB=\frac{p}{r}\).

Eventually:

\( p=qrB\)

We got to the heart of the topic. Once the charge of the particle \(q\) and the magnetic field \(\vec{B}\) are known, to get the momentum, we need to evaluate the curvature radius \(r\) of the track. This explains why detectors are often embedded in well controlled magnetic fields and tracking technologies are continuously developed.