Understanding precision, accuracy, and tolerance of geospatial datasets: an example based on the usage of GNSS receivers
Edited by Andrea Ajmar, with the contribution of Paolo Dabove, Lorenzo Galante, Fabio Giulio Tonolo, Elena Roglia
With this exercise you will learn the theoretical concepts related to precision, accuracy, and tolerance of spatial data and their impact on the results of GIS-based analysis. By means of a simple practical exersise, you will also try to assess the horizontal positional accuracy of GNSS positions acquired by means of mass market (i.e. smartphones or tablets) devices.
Errors in GIS data: definitions of precision, accuracy, and tolerance
This text is mainly extraxted from Understanding GIS Error, Accuracy, and Precision, and Metadata by Penn State – College of Earth and Mineral Sciences
It is generally recognized that error, inaccuracy, and imprecision can “make or break” many types of GIS projects. That is, errors left unchecked can make the results of a GIS analysis almost worthless.
The irony is that the problem of error devolves from one of the greatest strengths of GIS. GIS gain much of their power from being able to collate and cross-reference many types of data by location. They are particularly useful because they can integrate many discrete datasets within a single system. Unfortunately, every time a new dataset is imported, the GIS also inherits its errors. These may combine and mix with the errors already in the database in unpredictable ways.
The key point is that even though error can disrupt GIS analyses, there are ways to keep error to a minimum through careful planning and methods for estimating its effects on GIS solutions. Awareness of the problem of errors has also had the useful benefit of making GIS practitioners more sensitive to potential limitations of GIS to reach impossibly accurate and precise solutions.
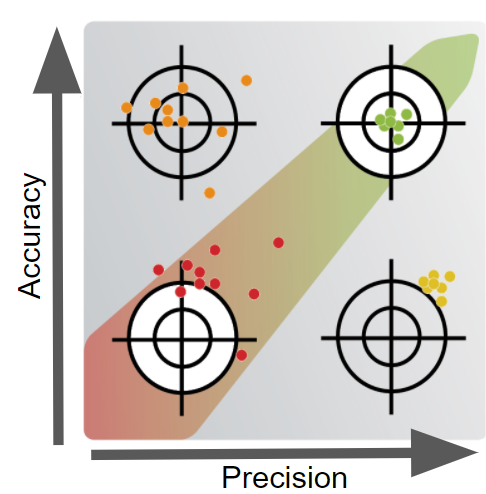
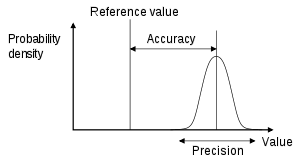
Precision is the degree of “convergence” (or “dispersion”) of data collected individually (sample) with respect to the average value of the series to which they belong or, in other words, their variance (or standard deviation) with respect to the sample mean. Therefore, if you measure the position of a point many times with an instrument, you have high precision when all the measurements you record are very close to each other. In GIS datasets, data precision is practically used to set the appropriate decimal precision for storing coordinates.
Accuracy is the deviation of a series of measurements from the real value. It is an issue that pertains both to the quality of the data collected and the number of errors contained in a dataset or a map. In discussing a GIS database, it is possible to consider horizontal and vertical accuracy with respect to geographic position, as well as attribute, conceptual, and logical accuracy.
Tolerance is normally defined in function of the precision: a convention generally valid in Italy set the tolerance, or in other words the acceptable error, as two times the value of the precision.
The level of precision and accuracy varies greatly for different applications. As high accuracy and high precision are both expensive, while planning a data survey/acquisition you must be fully aware of your application(s) requirements. And, as GIS analyst, you must be able to integrate your numerical results with their estimated accuracy, considering propagation and cascading effects.